The Big-o-notation - Quantifying complexity of algorithms

April 1st 2016

But it started simple…

As a programmer it is important to understand the impact of the algorithms you write. Simple logic may work well with limited datasets but can grow into a sluggish mess when working with larger datasets… The 'big-o-notation' enhances the programmer's awareness of the complexity his/her algorithms may create in worst case scenario's.

Bunny multiplication cartoon

The Big-O-Notation

The big-o-notation is a way to measure how well an algorithm scales as the amount of data involved increases. In sum: "How well will the algorithm behave with an array of 10 elements compared to an array of 10,000 elements?"
In such kind of notation, you will want to look at the worst possible outcome of your algorithm in order to identify (and optimize!) the bottlenecks in your code.

Different kinds of efficiency

In programming, there are often many ways to obtain a same outcome. In practice however your code is interpreted by the parser of your computer language and translated to binary calculations on the computer's processor. So as you may have guessed, each way of programming something will require different amounts of processing capacity. The big-o-notation classifies algorithms in 8 different categories of complexity:




Notation
(Most Efficient > Least efficient) 		Description Example Order (N = 100)
O(1) Time to complete is a constant Adding an element to an array: regardless of how many elements are already in the array, the time to complete is always the same 1
O(log N) The time to complete is logarithmic A binary search: For every search, the amount of data is halved, which makes it very efficient 6.64
O(N) Time to complete is in direct proportaion to the amount of data Linear search: Look in each element in the array
Because the big-o-notation searches for the worst possible outcome, it will consider each and every element in the array, not only the first match-case! 		100
O(N log N) log-linear: The log of N, multiplied by N. The time to complete is quasi-linear A typical example is a quicksort of the elements in a collection.
This number of comparisons equals log n! = log n + log(n-1) + log(n-2) + … + log(1) = n log n 		664
O(N2)
(quadratic) 		Time to complete is the square to the amount of data. A nested for-loop (2x)
for (… in …){
  for (… in …){
    //your code
   }
} 		10,000
O(N3) Time to complete is the amount of data to the power of three. A nested for-loop (3x)
for (… in …){
  for (… in …){
    for (… in …){
      //your code
    }
   }
} 		100,000
O(2N)
exponential 		The time to complete is exponential: If there are two solutions per element, the time to complete will be two to the power of N Solving the travelling salesman problem with dynamic programming ( a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions for later use) 1,267,650,600,228,230,000,000,000,000,000
O(N!) Factorial: The time to complet becomes very big very quickly Solving the travelling salesman problem with brute-force search (a very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's statement) 93,326,215,443,944,200,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000

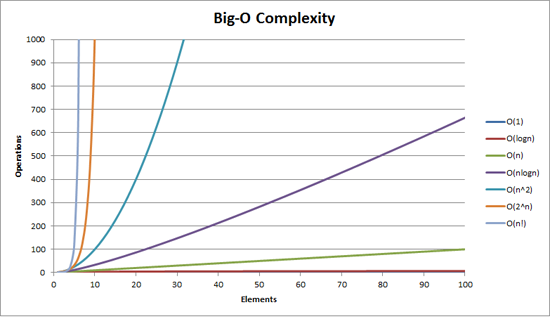
Big-o-notation graph

Just to give you an idea… If the numbers in the table represent seconds, you would be able to:

  • O(1): Count to one
  • O(log N): Go from 0 to 60 mph in 6.64 seconds BMW 325 sport edition.
  • O(N log N): Hard-cook an egg in a bit more than 11 minutes.
  • O(N2): Watch the Martian in 2 hours and 46 minutes.
  • O(N3): Watch the whole Harry Potter collection in 19h 47m (and have time to nap 8 hours).
  • O(2N: The time between today and the creation of the Earth approx. 4.02 Bn years ago… A trillion times!
  • O(N!): Euuhm… You get the picture right?

Fortunately, modern day personal computers often have multiple processors that are capable to perfom 2-3 million calculations per second (GHz), so we won't have to wait for eternity to load a page or run our programs.

Even if according to Moore's law, coputer powers doubles nearly every two years, it is advisable to think about efficiency of the algorithms you design… Especially if you intend to build successful applications that process data for many users!

References